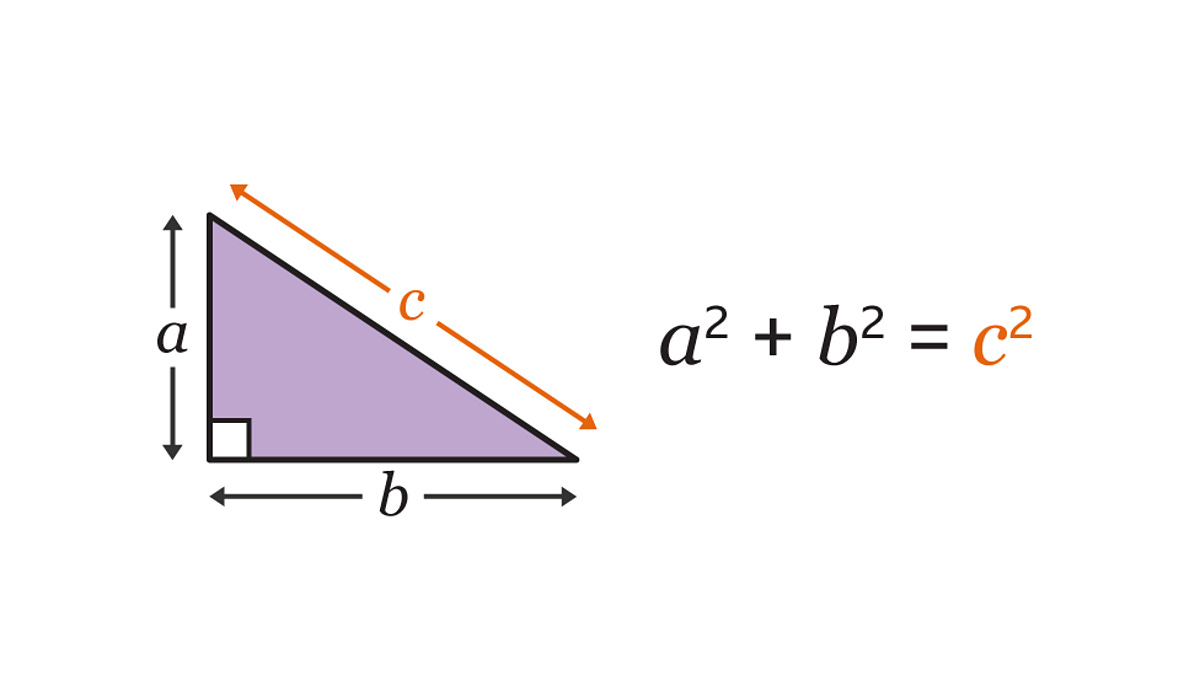În urma introducerii numerelor raționale, toate operațiile aritmetice fundamentale (adunarea, scăderea, înmulțirea și împărțirea) se pot efectua, fără depășirea „limitelor“; cu alte cuvinte, orice astfel de operație efectuată între numere raționale produce un nou număr rațional. Atunci ce nevoie am mai avea de încă o mulțime de numere și mai mare?
Radicali
Una dintre primele limitări descoperite de înțelepți pentru mulțimea numerelor raționale este că nu poate servi teoremei lui Pitagora, chiar într-un caz foarte simplu. Suma pătratelor lungimilor catetelor unui triunghi dreptunghic trebuie să fie egală cu pătratul lungimii ipotenuzei.
Cum grecii nu erau foarte interesați în geometrie de valori numerice și foloseau mai ales rigla negradată, au ajuns la următoarea problemă. Construim un triunghi dreptunghic care are catetele egale cu o unitate fiecare — adică lungimea unei rigle. Astăzi, am scrie acest lucru ca a = 1 și b = 1, în contextul imaginii de mai sus. Atunci ajungem la egalitatea c2 = 2 și niciun număr rațional nu poate avea o asemenea proprietate. Dincolo de faptul că un astfel de număr arată necesitatea lărgirii mulțimii numerelor raționale, problema ridicată a fost mult mai complicată din cauza teoriilor sacre ale pitagoreicilor, despre armonia adusă de numerele naturale și rapoartele lor — adică de numerele raționale. De aceea, numărul care ar avea o astfel de proprietate, c = √2, era nu doar o imposibilitate matematică, ci o erezie.
De-a lungul istoriei, matematicienii cu credințe ceva mai relaxate în ceea ce privește sacralitatea numerelor, au început să folosească numerele iraționale — acelea pentru care este imposibilă exprimarea sub forma unei fracții. Cele mai simple exemple au fost cele care se pot scrie sub forma unor radicali. De exemplu, putem construi triunghiul dreptunghic cu o latură a = 1 și una b = 2. Atunci ipotenuza c are proprietatea c2 = 5 și apare un nou număr irațional, c = √5.
Surprinzător sau nu, în context istoric, operația de extragere a radicalului nu era nouă în Grecia antică. S-au găsit mai multe tăblițe mesopotamiene și papirusuri egiptene care arată că aceste popoare cunoșteau operația, dar prin intermediul definiției sale: radicalul unui număr este acel număr pe care, dacă îl înmulțim cu el însuși, obținem numărul inițial. De exemplu, radicalul lui 2 este numărul care, înmulțit cu el însuși, îl dă pe 2: acel x pentru care x ∙ x = 2. Pusă problema astfel, pare ușor de înțeles în general, dar greu (de fapt, imposibil) de calculat practic. Însă dacă ne gîndim la radicalul unui număr ca 9, îl găsim imediat: 3 ∙ 3 = 9, deci √9 = 3. Popoarele antice puteau lucra cu ideea de radical, însă doar în cazuri simplu de calculat (precum 4, 9, 16, 25, 36 etc.) sau în aproximații: 1,41∙1,41 = 1,988, care era o aproximație bună, practică, pentru 2.

Constante universale
În afară de numerele scrise sub formă de radical, au mai apărut și altele care cereau extinderea mulțimii numerelor raționale: constantele universale. Aria cercului, de pildă, era cunoscută și ea din Antichitatea grecească, iar Arhimede scrisese despre raportul între lungimea și diametrul unui cerc, ca fiind o constantă universală, π. Valoarea lui π a fost calculată la fel cum s-a procedat și pentru √2. Mai multe dovezi arheologice arată că mesopotamienii și egiptenii foloseau valori ca 22/7 pentru π. Pentru scopuri practice primitive, eroarea este destul de mică: 22/7 = 3,1428, iar π ≅ 3,1415.
O altă constantă universală, cunoscută cel puțin implicit de popoarele Antichității începînd cu Grecia este așa-numitul număr de aur, φ. Valoarea lui exactă este (√5 + 1)/2, care face aproximativ 1,618. Numărul a fost folosit intuitiv de arhitecții Greciei antice, artiștii Renașterii și nu numai, lucru care i-a adus și numele, datorat armoniei pe care o arată o lucrare organizată ținînd cont de acest număr și care are ecouri și astăzi.
Dar, din moment ce popoarele Antichității nu puteau calcula și nici înțelege precis valoarea lui φ, ne putem întreba cum de era atît de prezent. Iar răspunsul vine dintr-un loc la fel de faimos, printr-o legătură demonstrată tîrziu: șirul lui Fibonacci. Sigur cunoașteți povestea: Leonardo, fiul lui Bonacci din Pisa (cca. 1200), propune un model matematic prin care modelează o populație de iepuri, pe parcursul generațiilor. Se ajunge la șirul: 1, 1, 2, 3, 5, 8, 13, 21,..., în care fiecare număr este obținut din suma precedentelor două. S-a demonstrat că, pe parcurs ce evoluează acest șir, dacă împărțim doi termeni consecutivi, ajungem să aproximăm din ce în ce mai bine numărul φ. Chiar 21/13 este o aproximație acceptabilă, 1,615.
În secolul al XVIII-lea, matematicianul elvețian Leonhard Euler (1707-1783) descoperă o nouă constantă universală, notată cu e, care astăzi îi poartă numele, cu valoarea aproximativă 2,718. Dacă π este ușor de prezentat cu ajutorul oricărui cerc, metoda folosită de Euler pentru a introduce numărul e este sofisticată și depășește scopurile acestui articol. Însă este suficient să spunem că nu după mult timp, numărul e a fost găsit ca fundamental pentru multe legi ale naturii (de la mecanica newtoniană la legea dezintegrării radioactive), motiv pentru care una dintre cele mai folosite operații care îl implică, logaritmul, s-a numit logaritm natural.
Există, desigur, și alte constante universale descoperite de matematicieni, cu aplicații mai mult sau mai puțin diverse. Cum rigoarea este valoarea supremă, provocarea următoare era să se demonstreze că niciuna dintre aceste constante nu se poate scrie ca un număr rațional, adică sub forma unei fracții. De exemplu, chiar π, care se definește prin raportul între lungimea și diametrul unui cerc, are această proprietate. Cu această ocazie și pe parcurs ce se înțelegeau tot mai bine numerele iraționale, apar numerele cu o infinitate de zecimale care nu se repetă și care se formează imprevizibil. O concluzie practică este că ne îndepărtăm de posibilitatea de a face calcule numerice exacte. Inginerii și toți cei care folosesc astfel de numere sînt nevoiți să recurgă la aproximații și, implicit, să accepte erori.
Continuitate
Valoarea exactă a numerelor iraționale a condus la o problemă conceptuală fundamentală în istoria ideilor: continuitatea. Faptul că putem construi un număr irațional cu o infinitate de zecimale, care apar după orice regulă dorim (fără să se repete la infinit, ca în cazul numerelor periodice) înseamnă că numerele iraționale pot „umple“ spațiul dintre orice două numere raționale. Și nu doar atît, ci că pot umple acest spațiu cu o infinitate de numere (iraționale). Simplificat, concluzia este că mulțimea numerelor reale — formată din mulțimea numerelor raționale, la care se adaugă cele iraționale și notată în matematică prin ℝ — acoperă fiecare punct de pe o dreaptă: axa numerelor reale. Oricît de mult am încerca să separăm punctele, apropiindu-ne cu zoom in, încă vom mai găsi puncte, chiar o infinitate, între cele pe care le credeam infinit de apropiate. Altfel spus, între orice două numere — raționale sau iraționale — încă mai putem găsi o infinitate de numere (raționale sau iraționale).
Această proprietate nu era adevărată pentru mulțimea numerelor raționale, care este tot infinită, dar se poate obține algoritmic:
pornim cu numerele naturale, care se pot enumera (primul, al doilea, al treilea etc.), asemenea pașilor unui algoritm;
adăugăm, pentru fiecare număr natural, varianta sa negativă și obținem mulțimea numerelor întregi;
alcătuim perechi de numere întregi (a, b), dar astfel încît al doilea număr să nu fie zero
și gata! Am obținut întreaga mulțime a numerelor raționale, cu pași clari, ce se pot implementa în principiu. Altfel spus, putem parcurge oricîți pași din listă; chiar dacă nu-i terminăm, fiecare pas este clar delimitat.
Dar cum s-ar putea obține un număr ca √2 sau π? Cu siguranță nu cu o astfel de procedură. Mai mult, însuși faptul că aceste numere sînt iraționale înseamnă că nu se poate găsi o procedură (de tip algoritmic) care să le producă, pornind de la numere raționale (implicit, și întregi, și naturale).
Ajungem la concluzia fascinantă că, deși mulțimea numerelor reale este infinită, ca și mulțimea numerelor raționale, între cele două nu există o corespondență unu la unu! Numerele reale sînt „mai multe“ decît cele raționale. Totodată, demonstrații ulterioare au arătat că, întrucît între orice două numere reale se mai găsește cel puțin (de fapt, o infinitate) de numere reale, ele se pot folosi pentru modelarea precisă, completă a axei numerelor. Mai mult chiar: aceste numere sînt suficiente pentru a exprima orice cantitate (distanță, lungime, timp etc.), motiv pentru care au ajuns să se numească numere reale.
Ideea continuității, apărută odată cu necesitatea numerelor reale, este strîns legată de o alta, fundamentală nu doar în științe: infinitul. Deja în rîndurile de mai sus am folosit-o, inevitabil. Pe lîngă infinitatea numerelor raționale sau reale, ideea infinitului apare și la scară mică, sub forma infinitezimalului. O cantitate mai mică decît cea mai mică la care vă puteți gîndi este o modalitate de a închipui infinitezimalul. Ideea de zoom in fără sfîrșit asupra unei drepte, a unor puncte urmărește același lucru: să tindă către o separare infinitezimală.
Ar fi o nedreptate istorică să spunem că ideea infinitului și cea a continuității au apărut odată cu numerele reale. Ele s-au dezvoltat pe parcursul mileniilor și găsim cîteva indicii chiar și în Antichitate. Și nu doar în matematică sau științe ale naturii, cît și în teologie, unde infinitul este asociat previzibil cu Divinitatea. Popoarele răsăritene au și ele o relație specială cu infinitul și continuitatea, care apar în filosofia specifică a transmigrației.
Nu am exagerat, deci, cînd am spus că aceste două idei — continuitatea și infinitului — sînt, poate, cele mai importante din istoria gîndirii umane, atît abstract, cît și concret, în sine și prin multitudinea de aplicații, în științe, filosofie, teologie, arte și matematică. De aceea, am decis să alcătuim un curs personalizat în care să discutăm despre aceste subiecte, cu un nivel de detalii potrivit fiecăruia dintre participanți.
Odată cu numerele reale, spuneam, putem exprima numeric „realitatea fizică“, o putem măsura și pune sub forma unor cantități. Unele dintre ele abstracte, imposibil de precizat complet, ca π, e și φ, iar altele, deja cunoscute din mulțimea numerelor raționale. Ce am putea dori mai mult?
Tocmai operația care a condus la numerele reale deschide calea către încă o extindere: radicalul. De ce să nu putem folosi această operație pentru numere negative? Este √-1 un număr? Și dacă da, în ce mulțime îl încadrăm? Iar dacă nu, ce legi fundamentale încalcă de nu merită locul printre celelalte numere?
Toate numerele sînt reale, doar că unele sînt mai reale decît altele. Despre celelalte, data viitoare.