Datorii
De unde să-ți dau, dacă n-am?
Pentru mulți dintre noi, primul contact cu numerele negative a fost sub forma unor „datorii“. Eram prea mici să înțelegem bilanțuri contabile sau greutățile împrumuturilor, dar am putut concepe un număr ca -2 precum o „lipsă de 2 lei“. Interpretarea rămîne și în afara școlii, fiindcă și băncile, contabilii și oamenii de finanțe notează cu numere negative orice pierdere sau datorie.
Dar să nu începem chiar cu atîta negativitate…
Istoric vorbind, operația de scădere este la fel de naturală (adică de relevantă în cotidian) ca și cea de adunare. Este de înțeles, deci, că popoarele preistoriei nu aveau nicio problemă să opereze cu scăderi; dar, tocmai pentru că erau ancorate în realitate, ele conțineau tot timpul un număr mai mic de scăzut dintr-unul mai mare — rezultatul fiind lesne de calculat și, mai important, pozitiv.
Apropo de calcule și operații, înainte să intrăm în alte detalii: pînă în preajma anilor 1600 ai erei noastre, cea mai mare parte a matematicii a circulat sub formă prozaică. Atunci cînd era vorba de probleme practice, precum comerțul sau împărțiri funciare, enunțurile, precum și toate calculele de rezolvare erau scrise cu tot contextul. Sigur, semnele operațiilor de adunare, scădere și altele, precum și simbolurile pentru cifre, erau cunoscute și folosite încă din perioada babiloniană — chiar dacă într-o formă diferită de cea din prezent, iar semnul pentru egalitate, apărut în calcule și ecuații, îl găsim prima dată în 1557, la Robert Recorde. Dar înțelepții și matematicienii popoarelor nu făceau pasul de abstractizare cunoscut astăzi. Enunțarea și rezolvarea problemelor erau la fel de mult exerciții de retorică, literatură și imaginație pe cît de matematică.
Un pas important, spre abstractizare în general și spre folosirea numerelor negative, a venit din China, în primul mileniu al erei noastre. Pînă atunci, babilonienii, egiptenii, indienii și celelalte popoare care foloseau matematica lucrau cu numere negative, dar indirect: doar în operații de scădere și doar cînd rezultatul era pozitiv. „Din trei saci de grîne, am consumat doi“, dar „Vecinul mi-a cerut cinci saci, iar eu am doar trei“ era inacceptabil (nu doar social). Situațiile care impuneau rezultate negative erau reformulate unde era posibil sau abandonate cu totul.
Un tip special de probleme face mai grea evitarea numerelor negative: sistemele de ecuații. Prozaic, ele se referă la cazuri cînd este necesar să ținem o evidență simultană a mai multor cantități interdependente. Un fel de C.A.R. în care atît contribuția, cît și dreptul de împrumut al fiecărui participant trebuie inventariate. Cantitățile necunoscute sînt mai multe și participă la numeroase interacțiuni, astfel că rezultatele pot fi imprevizibile.
Paranteză școlărească: Încă din clasele primare ne întîlnim cu astfel de probleme. Iată o formă tipică, pe care v-o propun ca scurtă gimnastică mintală:
Într-o ogradă avem găini și oi, în total 35 de animale. Dacă numărăm 110 picioare, cîte găini și cîte oi avem în ogradă?
Înțelepții chinezi au avut ideea să folosească bețișoare de culori diferite: dacă un număr se adună, se folosește un bețișor albastru; dacă se scade, unul roșu. Cu o astfel de reprezentare concretă, se va putea ține evidența cantităților foarte ușor (similar abacului, inventat cam în aceeași perioadă, de chinezi și de arabi). Mai mult — și mai important în discuția noastră —, o problemă care conducea la un rezultat final alcătuit doar din bețișoare roșii nu mai era respinsă ca „imposibilă“. Rezultatul era chiar foarte vizibil, iar culoarea îi dădea interpretarea necesară: un număr de scăzut din „nimic“, adică negativ. O lipsă, dar numai la nivel conceptual am spune acum, fiindcă prezența bețișoarelor este clară, iar culoarea lor arată, practic, doar o convenție ingenioasă.
Convenții
Exact așa ajungem la înțelesul modern al numerelor negative: ele arată intuitiv o absență, pentru că se obțin printr-o scădere, adică o deducere, o eliminare, dar, de fapt, această calitate este mai degrabă convențională. Între 3 și -3 există diferența conceptuală și convențională că unul se află de o parte a „originii numerelor“, zero, iar celălalt, de partea opusă.
Cantitățile negative, ca să folosesc un oximoron, arată, deci, convenții. Înălțimea de -1000m înseamnă adîncime de 1000m; deplasarea spre punctul A cu viteza de -1m/s înseamnă îndepărtare de A cu viteza de 1m/s; scăderea temperaturii (răcirea) cu -10 grade Celsius înseamnă creșterea ei (încălzirea) cu 10 grade Celsius1.
Toate aceste convenții se bazează pe referințe, care au ajuns universal acceptate. Înălțimile (pozitive) se măsoară în sus față de nivelul mării, temperaturile pozitive se măsoară în creștere de la punctul de îngheț al apei (pe scara Celsius), iar numerele pozitive se reprezintă pe o axă orizontală la dreapta față de un punct ales drept origine și reprezentînd numărul zero.
Această ultimă convenție este cu siguranță influențată de direcția de scriere a vesticilor, de la stînga la dreapta. Cercetătorul francez Stanislas Dehaene arată într-un studiu că studenții arabi situează numerele în ordine crescătoare de la dreapta la stînga atunci cînd răspund instinctiv, invers față de sistemul vestic. Mai mult, alți studenți arabi naturalizați aproximativ 10 ani în Franța pierd acest instinct și plasează numerele mai mari spre dreapta. Imaginea conceptuală a axei numerelor, cu tot cu direcția sa (de la dreapta la stînga sau invers) se studiază în psihologie și neuroștiințe sub numele de axă mintală a numerelor (mental number line).
Numerele negative nu reprezintă, însă, doar simple convenții culturale, sociale sau științifice. Abstract vorbind, în limbajul matematicii, scăderea este opusul (sau, dacă preferați, inversul) adunării. Înțelesul este cît se poate de practic. Cînd cineva aduce 3 mere pe o masă, ținem evidența prin 0 (niciun măr nu era prezent inițial) + 3 = 3, adică prin adunare. Operația mai poate fi gîndită și ca o transformare, o procedură de modificare a cantității de mere, un proces de mărire a cantității de substanță de pe masă. Dar acum, în limbajul tehnologiei, operația de “undo”, adică opusă, care ne aduce înapoi la starea anterioară este cea de eliminare a merelor, matematizată prin scăderea lor: 3 (mere prezente acum) - (din care elimin) 3 = 0 (nimic). Succesiunea este, deci:
Înțelese astfel, numerele negative devin opusele celor pozitive, „antidotul“ lor care, în sensul propriu, le anihilează, adică le transformă în zero, nimicul.
Rezultă de aici că nu întîmplător proprietățile fizice ale antiparticulelor din fizică sînt variantele opuse ale particulelor asociate. (Aproape) Toate caracteristicile devin „variantele cu minus“ ale celor pozitive. Nicăieri nu este mai ușor de văzut acest lucru decît în ce privește sarcina electrică sau curentul, în general. Inginerește vorbind, orice baterie sau generator de curent are două borne, puncte speciale de conexiune, notate (coincidență!) cu minus și plus. Direcția de curgere a curentului, adică de deplasare a electronilor în material este, în sensul fizic propriu, dinspre punctul (borna) minus către borna plus, la fel cum numerele cresc în aceeași direcție.
Dar mai e un motiv, la nivel atomic și molecular, pentru care materialele sau părți ale lor sînt notate cu plus sau minus. Electronul este unitatea fundamentală a sarcinii electrice negative2. Sarcina pozitivă este dată de protoni, iar moleculele ajung neutre cînd numărul de electroni este egal cu cel de protoni. Dar se pot produce și dezechilibre, naturale sau induse. Astfel apar ionii: pozitivi, dacă predomină protonii și negativi dacă predomină electronii.
Acum, deoarece natura preferă echilibrul, într-o substanță care conține ioni de ambele feluri sau într-un amestec alcătuit din substanțe în care predomină ioni opuși, electronii în plus ai părților negative vor migra spre părțile pozitive, pînă la stabilirea echilibrului. Dar deplasarea electronilor este chiar ceea ce formează curentul electric și așa se explică, pe scurt, funcționarea bateriilor electrice.
Perechile particulă-antiparticulă au corespondentul matematic în perechile de numere și opusele lor. Algebra abstractă, studiată în ultimul an de liceu, definește un număr ca -3 prin „opusul numărului 3, adică acel număr care, adunat cu 3, conduce la 0, numit și element neutru“. Abstractul acestei definiții permite folosirea ei cu minime modificări și pentru alte obiecte în afara numerelor: unde are loc o operație ca adunarea (și aceasta poate fi generalizată, dar e o altă discuție) și există un „element neutru“, care nu produce efecte cînd e folosit în adunare (similar numărului 0), putem defini opusul unui număr ca acela care îl anihilează și să-l notăm cu minus în față.
Evident că notațiile fac apel la intuiție și la cazul cel mai cunoscut, al numerelor întregi, dar matematica a putut generaliza și aceste obiecte.
Concluzia este că minusul care deosebește numerele negative de cele pozitive este, în natură, o convenție, iar matematic, un opus care anihilează perfect numărul natural (pozitiv) care-i corespunde.
Numere, în general
Variantele negative ale numerelor naturale, împreună cu cele pozitive, formează mulțimea numerelor întregi. Ea se notează matematic cu Z (scris cu un font special, de obicei: ℤ), datorită matematicienilor germani ai secolului al XIX-lea, care numesc Zahlen numerele în general. Atît de banale le-au părut numerele întregi încît le-au numit pur și simplu „numere“, iar Leopold Kronecker spunea în 1886:
Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.
(Dumnezeu a creat numerele întregi, toate celelalte sînt opera omului.)
Într-adevăr, numerele întregi alcătuiesc o continuare firească a celor naturale, astfel încît să permită și operații de scădere — adică de opoziție. Numite în engleză integers, ele nici nu mai lasă loc celor naturale în unele școli de gîndire: numerele naturale devin un simplu caz particular de întregi pozitivi, notate cu ℤ+.
Spus intuitiv și cumva filosofic, demersul matematicienilor a fost să elimine surpriza, să facă din noutate un lucru cunoscut. Pornim cu numere naturale, pe care le putem considera inevitabile în evoluția vieții și gîndirii umane, iar primele transformări sînt de a mări sau a micșora cantitățile de obiecte. Însă una dintre operații, aplicată „în principiu“, adică nu mereu practic, produce rezultate surprinzătoare: prea multe scăderi conduc la numere negative3. Ce e de făcut? Cea mai simplă reacție, care și îmbogățește matematica: modificăm mulțimile de numere cunoscute astfel încît să facem loc și celor noi.
Dar dacă am fi lucrat doar cu adunări și scăderi (i.e. adunări de opuse), matematica ar fi fost nu doar mai săracă, ci și mult mai laborioasă și mai puțin expresivă. Adunarea repetată se cheamă înmulțire, iar scăderea repetată este împărțire, așa că pasul următor este să ne întrebăm ce modificări aduc aceste operații cunoscute și folosite, practic, dintotdeauna.
De aceea găsesc mereu amuzant cînd ofertele comerciale se prezintă sub forma unor „reduceri de -10%“ — fiindcă, matematic vorbind, ele înseamnă creșteri de 10 procente! Cuvîntul „reducere“ deja implică o scădere, așa că o reducere cu un număr negativ devine o dublă negație și arată arată, de fapt, o adunare.
Motivul pentru care electronul este negativ constituie… ați ghicit, o convenție. Lucrul acesta nu arată o lipsă, ci doar o notație aleasă de Benjamin Franklin și păstrată pînă în zilele noastre.
Și cealaltă operație, adunarea, aplicată „de prea multe ori“, conduce la o altă surpriză: infinitul. Păstrăm discuția pentru altă ocazie.





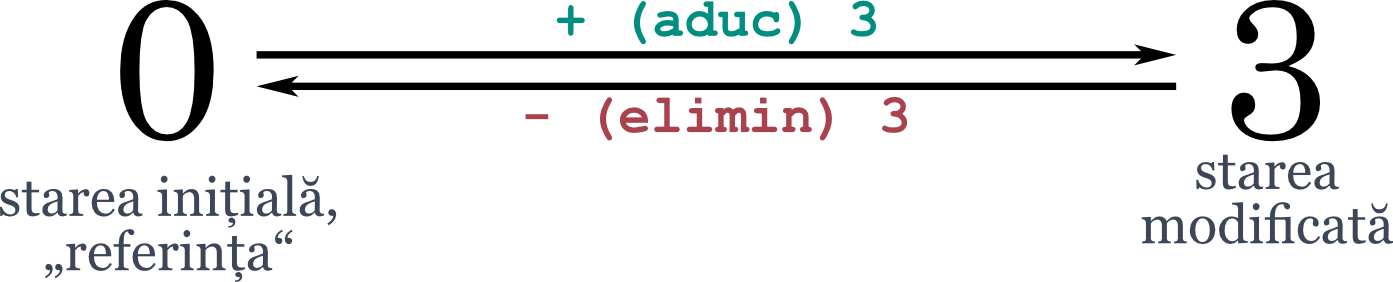
Lung articolul, dar foarte interesant in același timp