Simetria este o proprietate pe cît de naturală, pe atît de importantă în studii sofisticate și legi abstracte din matematică. Natura însăși prezintă numeroase ilustrări ale simetriei, însă ele sînt imperfecte — tocmai de aceea, rolul matematicii în definirea și utilizarea simetriei este unul formal, ideal. Dar creierele ni s-au adaptat atît de bine la aceste imperfecțiuni, încît aproximațiile sînt mai mereu suficiente. De exemplu, plasarea ochilor, a nărilor, a brațelor și picioarelor pare simetrică față de o axă imaginară care trece vertical, din creștet și pînă la bazin. Ne distrag atenția diformități pronunțate și rar conștientizăm că această simetrie bilaterală este aproape mereu imperfectă. Această aparență este, totuși, suficientă, întrucît studii psihologice au arătat că impresia unei fețe simetrice este suficientă pentru a o face mai atrăgătoare.
În continuare, traversăm cîteva domenii și subiecte în care simetria își arată profunzimea; de la istoria și etimologia cuvîntului, care ne conduc la vizual, dar și numeric, către psihologie și funcționarea minții. Evităm detalii matematice ori științifice sofisticate și vă invităm la prezentarea noastră din 1 aprilie, unde participarea este liberă și gratuită.
Simetric, asemenea, similar
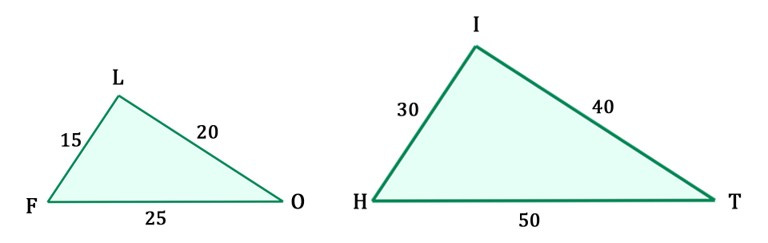
Etimologia simetriei trimite previzibil în Grecia antică, unde cuvîntul compus symmetria (συμμετρία) se traduce prin aceeași (sym) măsură (metron). Am putea crede că grecii priveau drept simetrice figuri care astăzi se numesc congruente — copii exacte. Dar înțelesul simetriei era mai subtil și se lega de armonia pe care o căutau pitagoreicii. Termenul potrivit este comensurabil, care se referă la mărimi sau cantități măsurabile cu aceeași unitate. De exemplu, un triunghi care are laturile de două ori mai mari decît un altul este comensurabil cu primul. O astfel de relație se numește în matematica elementară a zilelor noastre asemănare: două figuri se numesc asemenea dacă au laturile comensurabile[1]. Regăsim aici alte cuvinte din familia lexicală a simetriei, prin particula sim/sem: asemenea, similar.
Înțelesul simetriei a fost extins apoi către proporționalitate și relație a părții cu întregul. Cele două jumătăți ale unei figuri sînt proporționale cu figura întreagă, ceea ce le face simetrice.
Remarcăm că înțelesul simetriei pentru greci era strîns legat de măsurare și, prin extensie, de număr. Dictonul pitagoreic Totul este număr se potrivește perfect. Tocmai de aceea, apariția cazului ce privește diagonala unui pătrat a fost neașteptată: diagonala nu este simetrică față de latura pătratului, deși este o construcție naturală. Ea conduce la două triunghiuri dreptunghice simetrice, studiate de Pitagora. Numeric, raportul între diagonala unui pătrat și latura sa este egal cu radical din doi și chiar pentru nivelul avansat al studiului matematicii în Grecia antică, numărul este de neconceput. Pragul este cu atît mai mare cu cît această rupere a simetriei vine într-un context geometric simplu: acela al unui pătrat, o figură armonioasă, despre care se credea că este bine studiată.
Urmașii pitagoreicilor aduc mai multă generalitate în sensurile simetriei. Pînă în secolul al XVII-lea, ideea de simetrie se leagă tot de raportul între părți și întreg, dar permite și interschimbarea lor. Două părți ale unui întreg sînt simetrice dacă ele pot fi interschimbate, fără ca întregul să se modifice. Aceasta anticipează înțelesul modern al simetriei de reflexie, cum este cazul ochilor și membrelor corpului uman: pot fi interschimbate, dar oglindit. Totodată, forma revizuită nu mai ridică probleme în ce privește diagonala pătratului: cele două triunghiuri dreptunghice obținute sînt simetrice: se pot interschimba fără ca pătratul să se modifice, dar trebuie oglindite față de diagonală. Preocuparea pentru lungimea diagonalei nu mai este relevantă.
Modernizarea relaxează înțelesul strict al simetriei în termeni de măsurare, adică numerici și introduce o componentă vizuală. Interschimbarea părților în întreg este completată de observații comparative ale celor două perechi de direcții opuse: sus-jos, stînga-dreapta, care presupun împărțiri vizuale în raport cu axe imaginare care traversează figura. Cînd partea de sus — definită în raport cu o axă orizontală care trece prin mijlocul figurii — se poate schimba cu cea de jos (eventual oglindită), figura este simetrică.
Astfel ajungem aproape de înțelegerea prezentă a simetriei, pe care matematicianul german Hermann Weyl o formulează în anii 1900 cu ajutorul transformărilor:
Observ o figură, apoi ies din cameră. Dacă i se aplică o transformare în lipsa mea pe care îmi e imposibil să o remarc atunci cînd revin, transformarea respectivă este una de simetrie.
Tipare, texturi, detalii
În 1921, elvețianul Hermann Rorschach publică Psychodiagnostik, rezultatul de 174 pagini al unui studiu pe care l-a făcut cu zece cartonașe care conțin pete de cerneală presate prin îndoirea hîrtiei pe verticală. Modul de obținere face ca jumătățile figurilor să fie imagini reciproce în oglindă, deci le oferă o simetrie de reflexie.
Studiul, astăzi cunoscut ca testul Rorschach, cere pacienților să descrie imaginile de pe cartonașe, cu cît mai multe detalii. Unii comentează asupra aspectului de ansamblu, căruia îi asociază figuri cunoscute și spun că arată precum fluturi, oameni, păsări, alții se pot concentra pe texturi, aranjare, margini, culori. Apar și aprecieri subiective: păsările pe care le văd le par frumoase ori amenințătoare, chipurile sînt abstracte sau bine conturate.
Petele de pe cartonașe au fost alcătuite meticulos de Rorschach: cinci conțin doar cerneală neagră, două conțin cerneală neagră și roșie și trei, cerneluri multicolore.
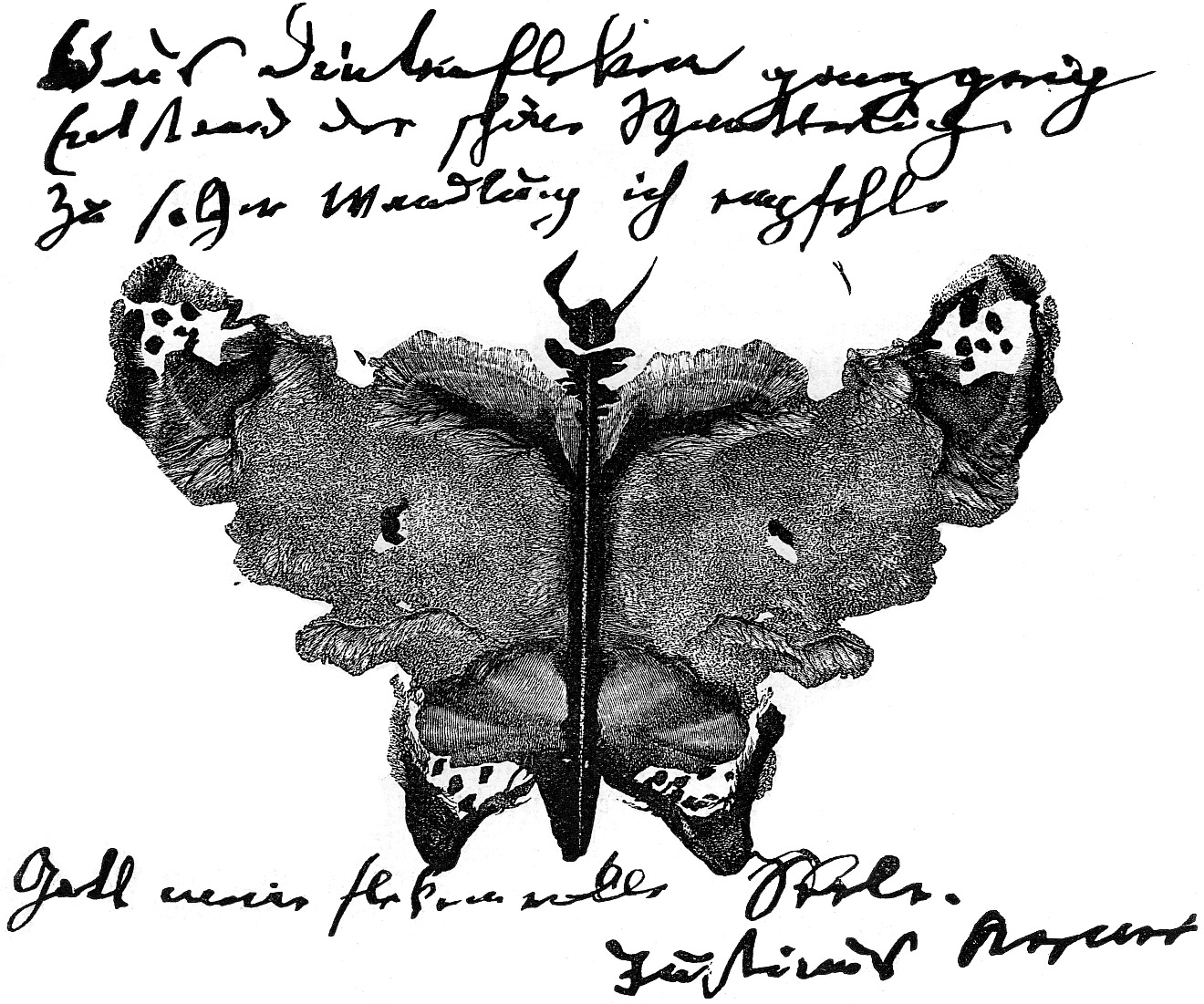
Ideea interpretării imaginilor ambigue nu este inventată de Rorschach. Leonardo da Vinci și Sandro Botticelli au inclus în lucrările lor figuri abstracte, intenționat ambigue. Descifrarea lor este personală, în sensul că dezvăluie trăsături psihologice ale privitorului. Mai tîrziu, în anii 1800, poetul german Justinus Kerner pune pete simetrice de cerneală în manuscrisele sale, printre poezii. Paginile cărților lui Kerner au fost numite klecksografii, de la cuvîntul german Klecks, pete.
Deși studiile lui Rorschach și relevanța testului său au fost și încă sînt disputate, cîteva lucruri sînt sigure. Creierul uman are două mecanisme care îl fac sensibil la astfel de teste. Primul, apofenia, este tendința de a vedea tipare. Cînd avem în față lucrări abstracte, căutăm instinctiv ordinea sau măcar ceva ce aduce a lucruri cunoscute. Aceste este însoțit de un altul, care ne ajută și în cazul matematicii: categorisirea. Dacă stimulii vizuali sînt prea mulți, neuronii sînt nevoiți să trimită informații diferite în lungul acelorași căi. Astfel, informațiile care ajung la același receptor sînt plasate în aceeași categorie, foarte general fie spus. De pildă, un obiect nemaivăzut, dar care are patru roți va fi categorisit automat drept un fel de vehicul; informațiile noi sînt prea multe, astfel că încercăm instinctiv să găsim tipare, lucruri cunoscute de care să ne legăm, iar cele patru roți ajută. Tocmai de aceea, imaginea de mai jos (generată cu inteligența artificială) a devenit virală în 2019: nu putem recunoaște nimic din ea.
Un alt mecanism, ceva mai rafinat, se numește pareidolie: tendința de a vedea fețe. Puteți găsi o întreagă comunitate de Reddit dedicată acestui fenomen. Nu-i așa că imaginea de mai jos arată o mașină ce se va răzbuna fiindcă a fost lăsată în frig?
Aceste procese nu au nimic patologic, însă mai multe studii au arătat că manifestarea lor exagerată se poate afla printre simptomele diverselor tulburări psihice. De exemplu, pacienții psihotici au o tendință pronunțată de a vedea și chiar de a căuta tipare în lucrurile din jur. În acest sens, studioul britanic Ninja Theory a lansat în 2017 jocul video Hellblade: Senua’s Sacrifice. Designerii au colaborat cu profesori de neuroștiințe de la Universitatea Cambridge și au încercat să pună jucătorul cît mai bine în pielea unui psihotic. Printre simptomele pe care le-au reprezentat este și tendința de a căuta tipare. Personajul-jucător, Senua, rezolvă puzzle-uri prin deplasarea în anumite locuri de pe hartă. Ea caută unghiurile potrivite din care privește obiectele din jur ca să descrie anumite rune.
Alte cercetări au arătat că o eventuală concentrare a pacientului supus testului Rorschach asupra texturilor, culorilor sau contururilor în defavoarea imaginii de ansamblu pot fi indicatori ai unor tulburări afective. Însăși ezitarea în descrierea imaginilor poate fi un indicator relevant.
Arome, stringuri, structuri
Simetria este o proprietate pe cît de naturală, pe atît de importantă în studii sofisticate și legi abstracte din matematică. Așa ar arăta o încheiere simetrică.
O completăm cu observația că am lăsat deoparte multe fenomene în care simetria produce rezultate surprinzătoare sau chiar impune legi ale naturii. Un exemplu este acela al moleculelor: imaginea în oglindă a uneia poate avea proprietăți diferite, iar un caz relevant este acela al limonenului. Aromă naturală găsită în coaja de lămîie, prin oglindirea ei se obține o moleculă otrăvitoare, care nu se găsește în natură și are o aromă de nucșoară.
Un alt domeniu plin de simetrii este acela al fizicii subatomice. Einstein și alți fizicieni au folosit simetria cu rol normativ: legile fizicii trebuie să fie simetrice, așa că o teorie care conține o forță exercitată doar de la dreapta la stînga trebuie să-și găsească un corespondent care să conțină o forță simetrică, de la stînga la dreapta. Ne-o spune chiar Newton, în principiul acțiunii și reacțiunii.
Aflați mai multe despre aceste subiecte, alte aplicații și exemple prin participarea la evenimentul nostru gratuit din 1 aprilie. El va fi urmat de cursul personalizat, cu începere din 17 aprilie și despre care puteți citi mai multe aici.
[1] Definiția matematică este ceva mai subtilă, dar pentru contextul acestui articol este suficientă această exprimare.