Rubrica Înscris, anunțată săptămîna trecută, debutează cu textul lui Mihnea Spiridon, elev în clasa a XI-a la Colegiul Național B. P. Hasdeu din Buzău, profilul matematică-informatică. Mihnea este, peste toate, un curios în tot ceea ce ține de știință. Are în portofoliu participări la olimpiadele naționale, activități de voluntariat și se pregătește din greu pentru a urma cursurile unei facultăți de informatică. Pentru relaxare, îi place să citească romane SF, favoritul său fiind Dune, de Frank Herbert.
Matematica este des privită drept o cutie neagră menită să producă ocazional povești ale unor oameni deveniți simboluri ale progresului. Atitudinea este una paradoxală — în plină revoluție digitală, mediul academic este foarte deschis, iar obscuritatea este rară. Istoria de astăzi ne va purta prin vremuri în care cunoașterea nu era la îndemîna oricui, așa cum este în vremurile noastre. Să pregătim scena.
Pe vremea primelor ecuații
Deși multe descoperiri contemporane încep drept curiozități intelectuale (matematicianul Godfrey H. Hardy se mîndrea că lucrările sale sînt lipsite de aplicabilitate practică), matematica a început cu rădăcinile în imediat, chiar în necesitățile cotidiene și gospodărești. Istoria dovedește că nevoia de a număra apare la începuturile tuturor societăților. Soluțiile pentru această trebuință sînt diverse, însă o dezvoltare suficientă a conceptelor conduce natural la ideea de ecuație. Etimologic, originea termenului este în latinescul aequare, care înseamnă egalare, iar egalitatea, cel puțin din punct de vedere matematic, este cea mai naturală relație între cantități.
Civilizațiile antice au descoperit, independent, concepte de matematică. Egiptenii se ocupau cu administrarea grînelor, pentru care adunarea și înmulțirea erau suficiente. Cu aceste operații se rezolvă problemele din papirusul Ahmes (cca. 2000 î.e.n), care propun cititorilor ecuația 5x/4 = 15. Rezultatul x = 12 este accesibil și apare ca soluție pentru o ecuație de gradul întîi. Acesta presupune înțelegerea ideii de necunoscută, de cantitate care trebuie aflată. S-au găsit chiar scrieri care folosesc pentru necunoscută un termen precis, aha, cu sensul de grămadă, cantitate. Găsim aici prototipul variabilelor din gîndirea matematică modernă.
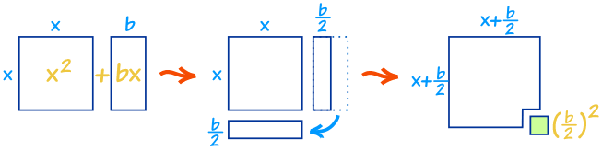
Babilonienii, chiar înaintea egiptenilor, împărțeau terenuri și aveau nevoie frecvent să găsească laturile unui dreptunghi de arie și perimetru dat. Scriau simultan cele două ecuații pentru perimetru și arie, P = 2x + 2y , respectiv A = xy, de unde se obținea după înlocuiri o singură ecuație de gradul doi, pătratică, de forma:
Intuiția lor geometrică purta numele de „completarea pătratului” și prevedea interpretarea lui ax2 la propriu, ca un pătrat. Termenul bx era împărțit în două dreptunghiuri cu o latură cunoscută (jumătate din b) ce se lipeau de acesta. Rămîne numai să adăugăm de ambele părți ale egalului cantitatea necesară pentru a umple pătratul mic din colț și să găsim latura pătratului mare ce se formează pentru a-l afla pe x. Nu era nevoie să memoreze nicio formulă, iar interpretarea vizuală (redată și în imaginea de mai jos) este cît se poate de practică!
O problemă de patru mii de ani
Dezvoltarea matematicii continuă cu contribuțiile arabilor, de la care au fost preluate numerele folosite astăzi (cifre arabe, cum sînt cunoscute, însă istoria arată că ele provin pe filieră indiană) și chiar denumirea de algebră (al-jabr). Au adus contribuții importante în diferite domenii, însă au întîlnit obstacole deosebite în rezolvarea ecuației de gradul al treilea, cubica. Arabii au tratat cu succes doar cîteva cazuri particulare, ceea ce surprinde, fiindcă soluțiile pentru ecuațiile de gradul întîi și doi sînt simple. Răspunsul la această problemă generală va veni în urma unui conflict memorabil din istoria matematicii, la peste patru milenii de la apusul civilizației lor, în Italia renascentistă.
Scipione dal Ferro găsește o formulă pentru ecuația cubică redusă, de forma:
dar moare în 1526 fără să o publice. Maestrul i-o lasă, totuși, studentului său, Antonio Fiore, care se mîndrește că ar fi descoperit-o singur. Fiore are îndrăzneala să îl provoace pe renumitul Niccolò Fontana Tartaglia la un duel public de matematică, cu speranța de a-l învinge prin cunoștințele sale exclusive.
Întîmplarea face că Tartaglia descoperise de unul singur formula pentru cubica redusă cu opt zile înaintea propunerii lui Fiore. El completa cubul, așa cum babilonienii completau pătratul, astfel că îl învinge cu ușurință pe învățăcel. Victoria lui Tartaglia îi aduce recunoaștere imediată și dovedește existența soluției. Aristocratul Gerolamo Cardano, doctor de profesie, dar amator al matematicii, este curios și pune presiuni asupra lui Tartaglia să dezvăluie secretul. Dorința îi este îndeplinită sub forma unui poem, transmis lui Cardano în schimbul jurămîntului de a nu dezvălui secretul.
Cardano utilizează formula lui Tartaglia pentru a descoperi rezolvarea cubicei complete. Ulterior, Cardano găsește în locuința seniorului dal Ferro o formulă ce o precede pe cea dată de Tartaglia — aceeași formulă pe care o cunoscuse și Antonio Fiore. Descoperirea îl face să se simtă liber de jurămînt, astfel că publică soluția în tratatul său din 1545, Ars Magna. Conflictul dintre Cardano și Tartaglia care a urmat, asupra drepturilor de autor pentru soluția cubicei, va rămîne în istorie.
Din grad în grad
Ars Magna a fost o adevărată revoluție. A inspirat generații de matematicieni și a deschis porțile cunoașterii cum au făcut-o puține scrieri dinaintea sa. Un exemplu remarcabil este cel al lui Lodovico Ferrari, care află cum să reducă ecuația de gradul al patrulea într-una de gradul al treilea. În cîțiva ani, au fost rezolvate două probleme aparent intratabile.
Atenția comunității matematice s-a îndreptat mai departe spre ecuația de gradul al cincilea, pe care italianul Paolo Ruffini și norvegianul Niels Abel au tratat-o în secolul al XIX-lea dintr-un alt unghi. Ei fac pași importanți spre demonstrația surprinzătoare că soluția nu există. Ideile lor au fost primite însă cu reticență și scepticism de către intelectualii vremii. Mai departe, dacă ecuația de gradul al cincilea nu putea fi rezolvată, ce se putea spune despre cea de gradul al șaselea? Dar despre ecuațiile de orice grad?
Acceptarea generală a ideilor lui Abel și Ruffini vine în urma contribuțiilor francezului Évariste Galois, care folosește ingenios și spectaculos idei proaspete ale algebrei, anume grupurile, studiate anterior izolat, de Joseph-Louis Lagrange și Arthur Cayley. Galois reușește să demonstreze, deci, riguros, că ecuații de grad mai mare sau egal cu cinci nu pot fi rezolvate în general, ceea ce încheie definitiv orice căutări ulterioare.
Teoria grupurilor a fost mai mult decît un artificiu de calcul. Ea își găsește în matematica de astăzi aplicații în aproape toate ramurile, mult mai multe decît și-ar fi imaginat vreodată Galois, dar și în chimie, fizică, biologie și chiar artă, fiind baza matematică a ideii de simetrie. Francezul a avut, însă, foarte puțin timp să viseze la evoluția teoriei sale, murind tragic la abia 20 de ani.
Atunci și acum
Multe s-au schimbat între timp în mediul academic. Publicațiile sînt esențiale astăzi, concurența a devenit mai loială, secretomania a dispărut, iar odată cu ea, și monopolul asupra metodelor de lucru. Atribuirea surselor este obligatorie, iar eforturile anti-plagiat se mișcă în ritm cu tehnologia.
Ideile noi precum cele ale lui Abel și Ruffini nu mai sînt tratate cu dispreț de o elită deja stabilită, ci sînt analizate fără prejudecăți. Geniile precum Galois sînt căutate și susținute prin pregătiri speciale, competiții și colaborări adaptate nivelului lor.
Recomandare: O prezentare accesibilă de ansamblu a istoriei ecuațiilor, care îl are în centru pe Galois, dar survolează milenii este cartea Ecuația care n-a putut fi rezolvată, scrisă de astrofizicianul de origine română Mario Livio și apărută la Humanitas în 2008.